सहसंबंध गुणांक (परिभाषा, सूत्र) - कैसे करें गणना?

सहसंबंध गुणांक क्या है?

सहसंबंध गुणांक का उपयोग यह निर्धारित करने के लिए किया जाता है कि दो चर के बीच संबंध कितना मजबूत है और इसके मूल्य -1.0 से 1.0 तक हो सकते हैं, जहां -1.0 नकारात्मक सहसंबंध का प्रतिनिधित्व करता है और +1.0 सकारात्मक संबंध का प्रतिनिधित्व करता है। यह चर में सापेक्ष आंदोलनों पर विचार करता है और फिर परिभाषित करता है कि उनके बीच कोई संबंध है या नहीं।

सहसंबंध गुणांक सूत्र

r = n ()xy) - nx /y / n (n * (∑x ² - (*x) ² )) * (n * (∑y ² - ()y ² )))

कहा पे

• r = सहसंबंध गुणांक
• n = टिप्पणियों की संख्या
• संदर्भ में x = 1 ^सेंट चर
• y = 2 ^{एन डी} चर

स्पष्टीकरण

यदि कोई सहसंबंध है या दो चर के बीच संबंध कहते हैं, तो यह इंगित करेगा कि यदि चर में से कोई एक मूल्य में बदलता है, तो दूसरा चर भी मूल्य में परिवर्तन करेगा, विशिष्ट में कहेंगे जो या तो उसी में हो सकता है या में हो सकता है विपरीत दिशा। समीकरण का अंश भाग एक साथ चलती चर की एक परीक्षण और सापेक्षिक शक्ति का संचालन करता है, और समीकरण का भाजक भाग वर्ग के चर से भिन्नता को गुणा करके अंश को मापता है।

उदाहरण

उदाहरण 1

निम्नलिखित दो चर, x और y पर विचार करें, आपको सहसंबंध गुणांक की गणना करने की आवश्यकता है।

नीचे गणना के लिए डेटा दिया गया है।

उपाय:

उपरोक्त समीकरण का उपयोग करते हुए, हम निम्नलिखित गणना कर सकते हैं

N = 4 के साथ उपरोक्त तालिका में हमारे सभी मूल्य हैं।

आइए अब सहसंबंध गुणांक की गणना के लिए मानों को इनपुट करें।

इसलिए, गणना इस प्रकार है,

आर = (4 * 25,032.24) - (262.55 * 317.31) / √ ((4 * 20,855.74) - (262.55) ² ) * ((4 * 30,058.55) - (317.31) ² )

r = 16,820.21 / 16,831.57

गुणांक होगा -

गुणांक = 0.99932640

उदाहरण # 2

कंट्री एक्स एक बढ़ती हुई अर्थव्यवस्था वाला देश है, और यह अपने केंद्रीय बैंक द्वारा ब्याज दरों में बदलाव के बारे में लिए गए निर्णयों का एक स्वतंत्र विश्लेषण करना चाहता है, चाहे उन लोगों ने मुद्रास्फीति को प्रभावित किया हो और केंद्रीय बैंक को नियंत्रित करने में सक्षम हो।

ब्याज दर के सारांश और उन वर्षों के लिए औसतन देश में प्रचलित मुद्रास्फीति दर नीचे दी गई है।

नीचे गणना के लिए डेटा दिया गया है।

देश के राष्ट्रपति ने आपसे एक विश्लेषण करने और अगली बैठक में उसी पर एक प्रस्तुति देने के लिए संपर्क किया है। सहसंबंध का उपयोग करें और निर्धारित करें कि केंद्रीय बैंक अपने उद्देश्य से मिला है या नहीं।

उपाय:

ऊपर चर्चा किए गए सूत्र का उपयोग करके, हम सहसंबंध गुणांक की गणना कर सकते हैं। ब्याज दर को एक चर के रूप में मानते हुए, x कहते हैं, और मुद्रास्फीति की दर को दूसरे चर के रूप में y के रूप में मानते हैं।

उपरोक्त तालिका में n = 6 के साथ हमारे सभी मूल्य हैं।

आइए अब सहसंबंध गुणांक की गणना के लिए मानों को इनपुट करें।

r = (6 * 170.91) - (46.35 * 22.24) / (((6 * 361.19) - (46.35) ² ) * ((6 * 82.74) - (22.24) ² )

आर = -5.36 / 5.88

सहसंबंध होगा -

सहसंबंध = -0.92

विश्लेषण: ऐसा प्रतीत होता है कि ब्याज दर और मुद्रास्फीति दर के बीच संबंध नकारात्मक है, जो सही संबंध प्रतीत होता है। जैसे ही ब्याज दर बढ़ती है, मुद्रास्फीति कम हो जाती है, जिसका अर्थ है कि वे एक दूसरे से विपरीत दिशा में चलते हैं, और यह उपरोक्त परिणाम से प्रकट होता है कि केंद्रीय बैंक ब्याज दर नीति से संबंधित निर्णय को लागू करने में सफल रहा।

उदाहरण # 3

एबीसी प्रयोगशाला ऊंचाई और उम्र पर अनुसंधान कर रही है और जानना चाहती है कि क्या उनके बीच कोई संबंध है। उन्होंने प्रत्येक श्रेणी के लिए 1000 लोगों का एक नमूना इकट्ठा किया है और उस समूह में औसत ऊंचाई के साथ आए हैं।

नीचे सहसंबंध गुणांक की गणना के लिए डेटा दिया गया है।

आपको सहसंबंध गुणांक की गणना करने और इस निष्कर्ष के साथ आने की आवश्यकता है कि यदि कोई संबंध मौजूद है।

उपाय:

आयु को एक चर के रूप में मानते हुए, x कहो और ऊँचाई (cms में) को एक अन्य चर के रूप में y के रूप में मानो।

उपरोक्त तालिका में n = 6 के साथ हमारे सभी मूल्य हैं।

आइए अब सहसंबंध गुणांक की गणना के लिए मानों को इनपुट करें।

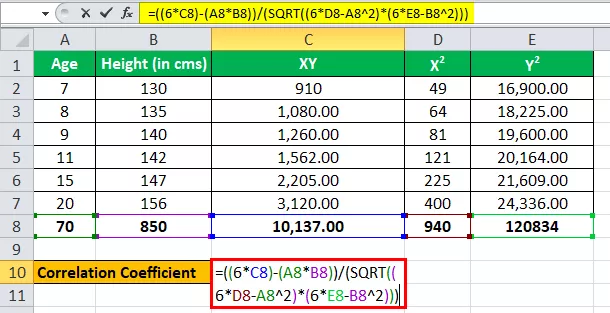
r = (6 * 10,137) - (70 * 850) / (((6 * 940 - (70) ² ) * ((6 * 1,20,834) - (850) ² )

आर = 1,322.00 / 1,361.23

सहसंबंध होगा -

सहसंबंध = 0.971177099

प्रासंगिकता और उपयोग

इसका उपयोग मुख्य रूप से आँकड़ों के बीच संबंधों की ताकत का विश्लेषण करने के लिए किया जाता है जो कि विचाराधीन हैं और आगे यह भी मापता है कि क्या डेटा के दिए गए सेटों के बीच कोई रैखिक संबंध है और वे कितनी अच्छी तरह से संबंधित हो सकते हैं। सहसंबंध में उपयोग किए जाने वाले सामान्य उपायों में से एक पियर्सन सहसंबंध गुणांक है।

यदि कोई चर मूल्य में परिवर्तन करता है और उसके साथ अन्य चर मूल्य में बदलता है, तो यह समझना कि संबंध महत्वपूर्ण है क्योंकि कोई व्यक्ति पूर्व चर के मूल्य का उपयोग बाद के चर के मूल्य में परिवर्तन की भविष्यवाणी करने के लिए कर सकता है। आज के इस आधुनिक युग में एक सहसंबंध के कई उपयोग हैं, जैसे कि इसका उपयोग वित्तीय उद्योग, वैज्ञानिक अनुसंधान और जहां नहीं किया जाता है। लेकिन, यह जानना महत्वपूर्ण है कि सहसंबंध के तीन प्रमुख प्रकार के संबंध हैं। पहला एक सकारात्मक संबंध है, जिसमें कहा गया है कि यदि किसी चर के मूल्य में परिवर्तन होता है, तो उसी दिशा में संबंधित चर में परिवर्तन होगा। इसी तरह, यदि कोई नकारात्मक संबंध है, तो संबंधित चर विपरीत दिशा में व्यवहार करेगा। इसके अलावा, अगर कोई सहसंबंध नहीं है, तो r एक शून्य मान होगा।अवधारणा को बेहतर ढंग से समझने के लिए नीचे दिए गए चित्र देखें।