सरल बचत कैलक्यूलेटर - व्यक्ति की परिपक्वता राशि की गणना

सरल बचत कैलकुलेटर के बारे में

सूत्र नीचे दिया गया है:

गणितीय रूप से इसकी गणना एक बार के साधारण बचत के लिए की जा सकती है:

दूसरी बात, यदि मासिक साधारण बचत की जाती है, तो गणना:

जिसमें,

• एम सरल बचत अवधि के अंत में कुल राशि है
• मैं निवेशित प्रारंभिक राशि हूं
• मैं नियमित अंतराल पर निवेश की गई निश्चित राशि है
• r ब्याज की दर है
• एफ ब्याज की आवृत्ति का भुगतान किया जाता है
• n उस अवधि की संख्या है जिसके लिए सरल बचत की जाएगी।

बहुत सारे बैंक और अन्य वित्तीय संस्थान हैं जो जमा को आकर्षित करने के लिए बाजार में प्रतिस्पर्धा कर रहे हैं ताकि वे अधिक व्यापार कर सकें, अर्थात, कॉर्पोरेट्स या उच्च निवल व्यक्तियों को पैसा उधार दें। कुछ बैंक ब्याज की उच्च दर का भुगतान करेंगे यदि जमा कुछ सीमा सीमा से अधिक है और खाते में बनाए रखा जाता है, या फिर, वे मानक दर का भुगतान करेंगे। इसके अलावा, ब्याज भुगतान की आवृत्तियों में अंतर हो सकता है; उदाहरण के लिए, ब्याज को बैंक के आधार पर त्रैमासिक, अर्ध-वार्षिक, या सालाना भुगतान किया जा सकता है। इसलिए, इस कैलकुलेटर के साथ, व्यक्ति यह निर्धारित करने में सक्षम होंगे कि वे किस वित्तीय संस्थान को अपनी धनराशि का निवेश परिपक्वता राशि या अपनी मूल राशियों पर अर्जित रिटर्न की तुलना करके करना चाहिए।

सरल बचत की गणना कैसे करें?

सरल बचत की गणना करने के लिए नीचे दिए गए चरणों का पालन करने की आवश्यकता है।

चरण # 1 - यह निर्धारित करें कि क्या राशि का निवेश किया जाएगा, चाहे वह एकमुश्त हो या एक आवधिक निवेश भी हो, तो बचत दरों की गणना में इसकी तुलना की जानी चाहिए।

चरण # 2 - व्यक्ति के लिए विकल्पों में उपलब्ध ब्याज की दर का पता लगाएं, और वह अर्जित किया जाएगा या साधारण बचत पर अर्जित होने की उम्मीद है।

चरण # 3 - अब, उस अवधि का निर्धारण करें जिसके लिए इसे निवेश किया जाएगा, और ज्यादातर उन लोगों के लिए लंबी अवधि के लिए होगा और मामले पर निर्भर करेगा।

चरण # 4 - ब्याज की दर को उस अवधि से विभाजित करें जब ब्याज या साधारण बचत ब्याज का भुगतान किया जाता है। उदाहरण के लिए, यदि भुगतान की गई दर 5% है और यह मासिक भुगतान करती है, तो ब्याज की दर 5% / 12 होगी, जो कि 0.416% है।

चरण # 5- अब उस सूत्र का उपयोग करें जो बिंदु 1 में ऊपर चर्चा की गई थी) यदि साधारण बचत राशि नियमित अंतराल पर बनायी जाती है तो सभी विकल्पों के लिए कोई प्रारंभिक राशि के साथ-साथ सामान्य बचत राशि बनायी जाती है। ।

चरण # 6 - परिणामी आंकड़ा परिपक्वता राशि होगी जिसमें साधारण बचत आय भी शामिल होगी और जिसने ब्याज के मामले में सबसे अधिक भुगतान किया है उसे चुना।

सरल बचत कैलकुलेटर उदाहरण

श्री विलियम अब एक वयस्क हैं और अपना पहला बचत खाता खोलने के लिए उत्साहित हैं। उसने वित्तीय संस्थान की तलाश की है, जो उच्च ब्याज दर प्रदान करता है, लेकिन वह हैरान है क्योंकि उसे नहीं मिलता है कि कौन सा बैंक उसे उच्चतम रिटर्न प्रदान करेगा। नीचे उद्धरण दिए गए हैं कि श्री विलियम ने शॉर्टलिस्ट किया है।

वह किसी एक खाते में $ 1,500 निवेश करना चाहता है, और वह उस तरह से निवेश करेगा जिस तरह से खाता ब्याज दे रहा है। उदाहरण के लिए, यदि बैंक अर्ध-वार्षिक भुगतान करता है, तो राशि प्रत्येक अवधि के अंत में समान रूप से निवेश की जाएगी और 10 वर्षों की अवधि के लिए ऐसा करना जारी रखेगा।

दी गई जानकारी के आधार पर, आपको उस राशि की गणना करने की आवश्यकता है जो वह बचत कर रही होगी, और उसी पर अर्जित ब्याज, और उसे किस बैंक में निवेश करना चाहिए।

उपाय:

हमें नीचे विवरण दिया गया है:

बैंक मैं

• I = प्रारंभिक राशि शून्य होगी
• r = ब्याज की दर जो 3.00% है और त्रैमासिक यह 3.00% / 4 होगी जो 0.75% है
• एन = आवृत्ति जो यहां त्रैमासिक है; इसलिए यह 4 होगा
• n = सरल बचत के वर्षों की संख्या, जो यहां 10 वर्ष है।
• i = यह निवेश की जाने वाली नियमित राशि है, जो 1500/4 है जो $ 375 है

अब, हम परिपक्वता राशि की गणना करने के लिए नीचे दिए गए सूत्र का उपयोग कर सकते हैं।

• = 0 * (1 + 0.75%) ^{10 * 4} + 375 * ((1 + 0.75%) ^{10 * 4} - 1 / 0.75%)
• = 17,417.43

परिपक्वता राशि 17,417.43 होगी

अर्जित ब्याज $ 17,417.43 - $ (375 * 40) = $ 2,417.43 होगा।

बैंक II

• I = प्रारंभिक राशि शून्य होगी
• r = ब्याज की दर जो 3.12% है और अर्ध-वार्षिक है वह 3.12% / 2 होगी जो 1.56% है।
• एन = आवृत्ति जो यहां अर्ध-वार्षिक है, इसलिए यह 2 होगी
• n = सरल बचत के वर्षों की संख्या, जो यहां 10 वर्ष है।
• i = यह निवेश की जाने वाली नियमित राशि है, जो 1500/2 है जो $ 750 है

अब, हम परिपक्वता राशि की गणना करने के लिए नीचे दिए गए सूत्र का उपयोग कर सकते हैं।

• = 0 * (1 + 1.56%) ^{10 * 2} + 750 * ((1 + 1.56%) ^{10 * 2} - 1) / 1.56%
• = $ 17,445.58

परिपक्वता मूल्य $ 17,445.58 होगा

अर्जित ब्याज $ 17,445.58 - ($ 750 * 20) = $ 2,445.58 होगा।

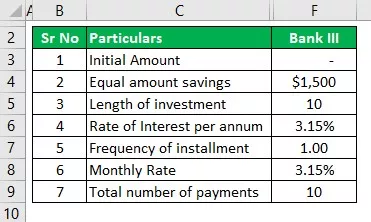
बैंक III

• I = प्रारंभिक राशि शून्य होगी
• r = ब्याज की दर, जो 3.15% है, और वार्षिक रूप से यह 3.15% / 1 होगी, जो 3.15% है
• एन = फ़्रिक्वेंसी जो वार्षिक रूप से यहां है, इसलिए यह 1 होगा
• n = सरल बचत के वर्षों की संख्या, जो यहां 10 वर्ष है।
• i = यह निवेश की जाने वाली नियमित राशि है, जो 1500/1 है जो $ 1,500 है

अब, हम परिपक्वता राशि की गणना करने के लिए नीचे दिए गए सूत्र का उपयोग कर सकते हैं।

• = 0 * (1 + 3.15%) ^{10 * 1} + 1500 * ((1 + 3.15%) ^{10 * 1} - 1) 3.15%
• = $ 17,315.08

परिपक्वता राशि $ 17,315.08 होगी

अर्जित ब्याज $ 17,315.08 - ($ 1500 * 10) = $ 2,315.08 होगा।

सबसे अधिक अर्जित राशि बैंक II में है, और इसलिए उसे बैंक II के साथ एक खाता खोलना चाहिए।

निष्कर्ष

यह कैलकुलेटर, जैसा कि ऊपर चर्चा की गई है, का उपयोग वित्तीय संस्थान में विभिन्न परिपक्वता मात्राओं की तुलना करने के लिए किया जा सकता है क्योंकि ब्याज की उच्च दर उच्चतम निरपेक्ष राशि की गारंटी नहीं देती है, जैसा कि ऊपर दिए गए उदाहरण में देखा गया है। इसलिए, किसी को परिपक्वता के दौरान राशियों की गणना और तुलना करनी चाहिए और फिर निर्णय लेना चाहिए।