यौगिक (परिभाषा, उदाहरण) - कंपाउंडिंग की शक्ति

यौगिक परिभाषा

चक्रवृद्धि ब्याज दर की गणना करने की विधि है जो प्रभावी रूप से ब्याज पर ब्याज है जहां ब्याज की गणना निवेश पर की जाती है / आरंभिक मूलधन और ब्याज पर ब्याज और अन्य पुनर्निवेश, दूसरे शब्दों में अर्जित ब्याज जमा या ऋण की समयावधि के आधार पर मूल राशि में जमा होता है। यह मासिक, त्रैमासिक या वार्षिक हो सकता है

आइए समझने की कोशिश करें कि कुछ बुनियादी उदाहरणों के माध्यम से क्या जटिल है और यह कैसे काम करता है

कंपाउंडिंग की शक्ति के शीर्ष 4 उदाहरण

उदाहरण 1

शेन और मार्क दोनों ने $ 1,00,000 का निवेश करने का फैसला किया, लेकिन शेन ने साधारण ब्याज में निवेश करने का फैसला किया, जबकि मार्क 10 साल के लिए दस साल के लिए चक्रवृद्धि ब्याज में निवेश करता है। देखते हैं दस साल बाद क्या होता है।

उपाय:

तो, शेन निवेश की गणना होगी -

कुल कमाई राशि = $ 200,000

साधारण ब्याज के साथ, शेन को 10 साल बाद 2,00,000 डॉलर मिलेंगे।

चिह्न निवेश की गणना होगी -

कुल कमाई राशि = $ 2,59,374

चक्रवृद्धि ब्याज के साथ, मार्क का निवेश मूल्य $ 2,59,374 हो जाएगा।

अब शेन ने मार्क जैसी कंपाउंडिंग विधियों के माध्यम से निवेश करने का फैसला किया और दोनों ने $ 15% की दर से $ 2,00,000 का निवेश किया।

शेन निवेश की गणना होगी -

कुल कमाई राशि = $ 8,09,111.55

शेन 10 साल के लिए निवेश करता है और 15% की दर से $ 8,09,111.55 के रूप में अंतिम राशि प्राप्त करता है।

चिह्न निवेश की गणना होगी -

कुल कमाई राशि = $ 65,83,790.52

हालांकि, मार्क लंबी अवधि के निवेशकों के लिए धैर्य है और 25 साल के लिए निवेशित रहता है, और उनका निवेश मूल्य $ 65,83,790.52 हो जाता है

ऊपर दिए गए उदाहरण से कंपाउंडिंग की शक्ति का पता चलता है। निवेश क्षितिज जितना लंबा होगा, घातीय वृद्धि होगी।

उदाहरण # 2 (साप्ताहिक)

साइमन के पास बचत में 7500 डॉलर हैं, और अपने बेटे के कॉलेज फंड के लिए, जो 15 साल बाद कॉलेज में भाग लेने जाएगा, उसने यूएस सेविंग बॉन्ड्स में निवेश करने का फैसला किया। साइमन का लक्ष्य $ 20,000 बचाना है, और अमेरिकी बचत बांड के लिए वार्षिक प्रतिशत दर 6% है। 15 वर्षों के बाद साइमन मनी का भविष्य मूल्य क्या है?

उपाय:

दिया हुआ,

• प्रिंसिपल = $ 7500
• दर = 6% या 0.06
• समयावधि = 15 वर्ष।
• एक वर्ष n = 52 सप्ताह में इसे कितनी बार मिश्रित किया जाता है
• भविष्य का मूल्य =?

तो, भविष्य के मूल्य की गणना होगी -

साप्ताहिक कंपाउंडिंग का फॉर्मूला नीचे दिया गया है।

एफ = पी (1 + आर / एन) एन * टी

• F = $ 7500 (1 + 0.06 / 52) 52 * 15
• F = $ 7500 (1 + 0.001153846) 780
• एफ = $ 18,437.45

इसलिए उपरोक्त गणना से, यह स्पष्ट है कि $ 20,00 को बचाने के लिए साइमन का लक्ष्य उपरोक्त तरीकों से प्राप्त नहीं होगा, लेकिन यह उसके करीब है।

निरंतर यौगिक विधि

अब चलिए कंटीन्यूअस कंपाउंडिंग फॉर्मूला के साथ उपरोक्त उदाहरण को आजमाते हैं।

तो, भविष्य के मूल्य की गणना होगी -

एफ = पे आर * टी

• F = $ 7500e 0.06 * 15
• F = $ 7500e 0.9
• भविष्य का मूल्य (F) = $ 18,447.02

अब कंटिन्यूअस कंपाउंडिंग के साथ भी, सिमोन के अपने बेटे के कॉलेज फंड के लिए 20,000 डॉलर की बचत का लक्ष्य हासिल नहीं होगा।

आइए, मंथली कम्पाउंडेड फॉर्मूला के साथ देखें कि 15 साल में 20,000 डॉलर बचाने के अपने लक्ष्य को हासिल करने के लिए 6% के APR के साथ साइमन को कितने पैसे की जरूरत थी?

तो, भविष्य के मूल्य की गणना होगी -

एफ = पी (1 + आर / एन) एन * टी

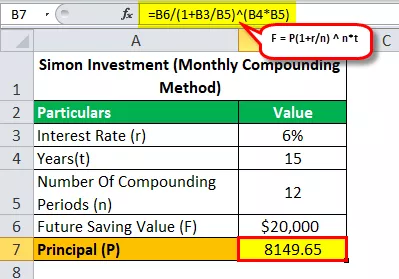
• $ 20,000 = पी (1 + 0.06 / 12) 12 * 15
• पी = $ 20,000 / (1 + 0.06 / 12) 12 * 15
• प्रिंसिपल (पी) = 8149.65

इसलिए उपरोक्त समीकरण को हल करने से, हमें एक उत्तर मिलेगा जो $ 8,149.65 है (राशि, जिसे साइमन को 15 वर्षों में $ 20,000 बचाने के अपने लक्ष्य को प्राप्त करने के लिए निवेश करने की आवश्यकता है)।

उदाहरण # 3 (प्रभावी वार्षिक यील्ड)

मान लें कि एक्सवाईजेड सीमित बैंक वरिष्ठ नागरिकों को फिक्स्ड डिपॉजिट के लिए 10% प्रति वर्ष देता है, और हम यहां मानते हैं कि बैंक ब्याज अन्य सभी बैंकों की तरह तिमाही चक्रवृद्धि है। 5, 7 और 10 वर्षों के लिए प्रभावी वार्षिक उपज की गणना करें।

उपाय:

5 साल के लिए वार्षिक यील्ड:

• टी = 5 साल
• n = 4 (त्रैमासिक मिश्रित)
• I = 10% प्रति वर्ष

तो ए = (१ + १०% / १०० / ४) (५ * ४)

• ए = (1 + 0.025) 20
• ए = 1.6386
• 5 साल में मैं = 0.6386

प्रभावी ब्याज = 0.6386 / 5

प्रभावी I = 12.772% प्रति वर्ष

7 साल के लिए वार्षिक यील्ड:

• t = 7 वर्ष
• n = 4 (त्रैमासिक मिश्रित)
• I = 10% प्रति वर्ष

अतः ए = (१ + १०% / १०० / ४) () * ४)

• ए = (1 + 0.025) 28
• ए = 1.9965
• 7 साल में मैं = 1.9965
• प्रभावी I = 0.9965 / 7

प्रभावी I = 14.236% प्रति वर्ष

10 वर्षों के लिए वार्षिक यील्ड:

• t = 10 वर्ष
• n = 4 (त्रैमासिक मिश्रित)
• I = 10% प्रति वर्ष

तो ए = (१ + १०% / १०० / ४) (१० * ४)

• ए = (१ + ०.०२५) ४०
• ए = 2.685
• 10 वर्षों में I = 1.685
• प्रभावी I = 1.685 / 10

प्रभावी I = 16.85% प्रति वर्ष

उदाहरण # 4 - (वार्षिकियां: भविष्य का मूल्य)

$ 1,000 का निवेश हर 3 महीने में 4.8% प्रतिवर्ष के हिसाब से किया जाता है। 10 वर्षों में वार्षिकी का मूल्य कितना होगा?

उपाय:

इसलिए जब हम कहते हैं कि 10 वर्षों में वार्षिकी का मूल्य कितना होगा, तो इसका मतलब है कि हमें भविष्य का मूल्य खोजना होगा, और यह महत्वपूर्ण है क्योंकि जब भी वार्षिकी पर एक उदाहरण होता है, तो हमें यह देखना होगा कि हमें क्या पता लगाना है।

तो, Future Value का सूत्र है

वार्षिकी का FV = P ((1+ r) ⁿ - 1 / r)

• पी = आवधिक भुगतान
• आर = दर प्रति अवधि
• n = अवधियों की संख्या

तो Future Value का सूत्र है

• तो यहाँ P = $ 1,000
• आर = 4.8% प्रति वर्ष या 0.048
• r (त्रैमासिक) = 0.048 / 4
• r (त्रैमासिक) = 0.012
• n = 10 वर्ष
• n (कंपाउंडिंग की संख्या लागू होगी) = 10 × 4 = 40

तो, वार्षिकी की FV की गणना होगी -

तो अब FV = $ 1000 (1 + 0.012) 40 -1 / 0.012)

तो उपरोक्त समीकरण को हल करने से $ 50,955.30 का FV मिलेगा

तो 10 वर्षों में वार्षिकी कितनी होगी और उत्तर $ 50,955.30 है

इसके अतिरिक्त, हम उपरोक्त उदाहरण से भी पता लगा सकते हैं कि 10 वर्षों में कितना ब्याज अर्जित किया गया है।

जैसा कि 40 गुना $ 1000 का निवेश किया जाता है जो कुल निवेश (40 × $ 1000 = $ 40,000) है।

तो ब्याज = भविष्य का मूल्य - कुल निवेश

• ब्याज = $ 50,955.30 - $ 40,000
• ब्याज = $ 10,955.30

इसलिए यहां यह समझना जरूरी है कि एन्युइटीज में निवेशक काफी ब्याज कमा सकते हैं। उपरोक्त विशेष उदाहरणों में, $ 40,000 का एक जमा, बदले में, $ 10,955.30 का कुल ब्याज देता है।

नोट: आप विस्तृत गणना के लिए ऊपर दिए गए एक्सेल टेम्पलेट डाउनलोड कर सकते हैं।